Una vez recibidos los datos procedentes del AEMET, se procedió a realizar resúmenes promediando las series decenales y obteniendo la siguiente tabla resumen con las estaciones, los meses y las temperaturas medias correspondientes.
A la hora de modelizar la temperatura, el valor de esta variable en un punto dado va a depender no tanto de la distancia a los puntos con temperatura conocida, sino de otros factores geográficos como son, principalmente, la altura y la distancia al mar. Es lo que se conoce como regresión ponderada geográficamente (GWR por sus siglas en inglés). En el caso de Gran Canaria, al ser un territorio limitado y de fuertes pendientes, el efecto de la altura sobre el diferencial de temperatura está altamente relacionado, mientras que el factor de distancia a la costa (usado en modelos continentales) es, en este caso, despreciable.
Aparte de esto, y de acuerdo con la publicación Sostenibilidad Energética de la Edificación en Canarias. Manual de Diseño (García de Diego, Margarita de Luxan; Reymundo Izard, Araceli;, 2011), hay que tener en cuenta el factor vertiente, ya que por el efecto de los vientos alisios, los lugares situados en la cara norte pueden tener un gradiente de temperaturas distinto a los expuestos en la cara sur. Para ello, se clasificaron las estaciones según la vertiente, estableciendo un eje formado por cuatro estaciones que formarían parte de ambas vertientes.
Por lo tanto, es siguiente paso fue plantear la relación entre altura y temperatura de la forma más sencilla, que es mediante una regresión lineal simple. Para comprobar si este tipo de regresión es la más adecuada se calcularon los índices de correlación entre dichas variables según la siguiente fórmula en función de la temperatura T y la altura Z:
Los resultados, teniendo en cuenta las vertientes y separado por meses se pueden ver en la siguiente figura:
Del análisis de los resultados se puede deducir lo siguiente:
· Los valores son negativos por lo que se confirma que la temperatura disminuye con al altura
· En general, existe un alto grado de correlación entre las variables excepto en los meses de verano.
· Los índices empeoran si no se tiene en cuenta el factor vertiente.
Como la regresión lineal simple no ofrece resultados satisfactorios para el conjunto de los meses se procedió a realizar un ajuste mediante un polinomio de grado 2 de forma que la temperatura de un punto P dado vendrá dada por la expresión:
Los valores de los índices a,b y c se calcularon en el software MatLAB mediante mínimos cuadrados para cada uno de los meses y vertientes. Para evitar problemas de condicionamiento de matrices durante el ajuste, se realizó una normalización de las variables mediante la media m y la desviación estándar d, por lo que la fórmula de ajuste quedaría:
Obteniendo los siguientes resultados:
donde el valor rms corresponde con el error medio cuadrático resultante en cada uno de los ajustes dado en decimas de grado. En la siguiente figura se muestra como ejemplo una gráfica de la curva de ajuste correspondiente al mes de mayo, vertiente norte.
La bondad del ajuste realizado viene dado por el índice de correlación para regresiones cuadráticas mediante la siguiente fórmula que relaciona los valores de a y b calculados, el número n de pares temperatura-altura y los sumatorios de los valores T y Z :
Al igual que en el caso de la regresión lineal simple, se procedió a calcular los índices de correlación tanto por meses como por vertientes. En la siguiente figura se muestran los valores obtenidos comparados con los obtenidos con la regresión lineal simple.
A la vista de los resultados obtenidos se puede concluir lo siguiente:
· Los índices de correlación del ajuste cuadrático son mejores que los del ajuste lineal, especialmente en los meses de verano.
· También en este caso, el hecho de no tener en cuenta las vertientes empeora los resultados.
· La bondad de los valores calculados para el ajuste cuadrático por vertientes se considera suficiente.
A la hora de calcular cada uno de los mapas se tuvo en cuenta al recorrer el MDE en que vertiente estaba el punto calculado para utilizar los coeficientes correspondientes. Entre las 986 filas del MDE se estableció el cambio de vertiente en la fila número 450 contada desde la más septentrional, que coincide aproximadamente con la coordenada Y de las estaciones utilizadas como eje. Para evitar el efecto frontera que produciría un cambio drástico de coeficientes al pasar de la fila límite a la siguiente, se usaron los coeficientes de ambas vertientes desde la fila 400 a la 500, ponderando en cada caso en función a la distancia al eje como se muestra en el esquema de la siguiente figura:
La fórmula utilizada para la ponderación en los límtes de vertientes fue la siguiente:
Donde Tfinal es la temperatura final calculada, Tnorte es la temperatura calculada por la vertiente norte, Tsur es la temperatura calculada por la vertiente sur y nf es el número de fila.
Con estos datos, se procedió mediante el software MatLAB al cálculo del mapa mensual de temperaturas medias para cada uno de los meses, y que a modo de ejemplo se muestra en la siguiente figura el correspondiente al mes de mayo.
En la siguiente imagen se muestra la evolución de los valores medios de la temperatura por meses:
Las12 imágenes del mapa obtenido se pueden ver aqui.
Enlaces de interés:
Anterior: Carta bioclimática de Olgyay
Siguiente: Mapa mensual de Humedad Relativa
 |
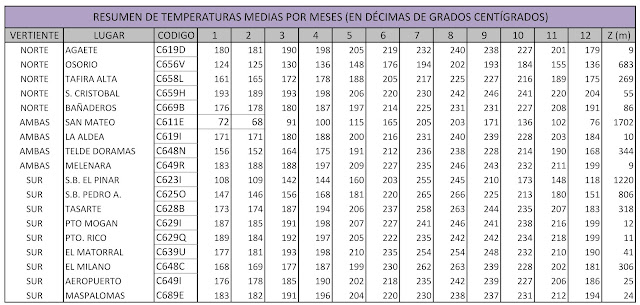| Resumen de Temperaturas Medias mensuales |
A la hora de modelizar la temperatura, el valor de esta variable en un punto dado va a depender no tanto de la distancia a los puntos con temperatura conocida, sino de otros factores geográficos como son, principalmente, la altura y la distancia al mar. Es lo que se conoce como regresión ponderada geográficamente (GWR por sus siglas en inglés). En el caso de Gran Canaria, al ser un territorio limitado y de fuertes pendientes, el efecto de la altura sobre el diferencial de temperatura está altamente relacionado, mientras que el factor de distancia a la costa (usado en modelos continentales) es, en este caso, despreciable.
Aparte de esto, y de acuerdo con la publicación Sostenibilidad Energética de la Edificación en Canarias. Manual de Diseño (García de Diego, Margarita de Luxan; Reymundo Izard, Araceli;, 2011), hay que tener en cuenta el factor vertiente, ya que por el efecto de los vientos alisios, los lugares situados en la cara norte pueden tener un gradiente de temperaturas distinto a los expuestos en la cara sur. Para ello, se clasificaron las estaciones según la vertiente, estableciendo un eje formado por cuatro estaciones que formarían parte de ambas vertientes.
 |
| Clasificación de estaciones AEMET por vertientes |
 |
| Clasificación de estaciones por vertientes |
Por lo tanto, es siguiente paso fue plantear la relación entre altura y temperatura de la forma más sencilla, que es mediante una regresión lineal simple. Para comprobar si este tipo de regresión es la más adecuada se calcularon los índices de correlación entre dichas variables según la siguiente fórmula en función de la temperatura T y la altura Z:
Los resultados, teniendo en cuenta las vertientes y separado por meses se pueden ver en la siguiente figura:
 |
| Índices de correlación lineal entre alturas y temperaturas por meses y vertientes |
Del análisis de los resultados se puede deducir lo siguiente:
· Los valores son negativos por lo que se confirma que la temperatura disminuye con al altura
· En general, existe un alto grado de correlación entre las variables excepto en los meses de verano.
· Los índices empeoran si no se tiene en cuenta el factor vertiente.
Como la regresión lineal simple no ofrece resultados satisfactorios para el conjunto de los meses se procedió a realizar un ajuste mediante un polinomio de grado 2 de forma que la temperatura de un punto P dado vendrá dada por la expresión:
donde el valor rms corresponde con el error medio cuadrático resultante en cada uno de los ajustes dado en decimas de grado. En la siguiente figura se muestra como ejemplo una gráfica de la curva de ajuste correspondiente al mes de mayo, vertiente norte.
 |
| Curva de ajuste correspondiente al mes de mayo, vertiente norte |
Al igual que en el caso de la regresión lineal simple, se procedió a calcular los índices de correlación tanto por meses como por vertientes. En la siguiente figura se muestran los valores obtenidos comparados con los obtenidos con la regresión lineal simple.
A la vista de los resultados obtenidos se puede concluir lo siguiente:
· Los índices de correlación del ajuste cuadrático son mejores que los del ajuste lineal, especialmente en los meses de verano.
· También en este caso, el hecho de no tener en cuenta las vertientes empeora los resultados.
· La bondad de los valores calculados para el ajuste cuadrático por vertientes se considera suficiente.
A la hora de calcular cada uno de los mapas se tuvo en cuenta al recorrer el MDE en que vertiente estaba el punto calculado para utilizar los coeficientes correspondientes. Entre las 986 filas del MDE se estableció el cambio de vertiente en la fila número 450 contada desde la más septentrional, que coincide aproximadamente con la coordenada Y de las estaciones utilizadas como eje. Para evitar el efecto frontera que produciría un cambio drástico de coeficientes al pasar de la fila límite a la siguiente, se usaron los coeficientes de ambas vertientes desde la fila 400 a la 500, ponderando en cada caso en función a la distancia al eje como se muestra en el esquema de la siguiente figura:
La fórmula utilizada para la ponderación en los límtes de vertientes fue la siguiente:
Donde Tfinal es la temperatura final calculada, Tnorte es la temperatura calculada por la vertiente norte, Tsur es la temperatura calculada por la vertiente sur y nf es el número de fila.
Con estos datos, se procedió mediante el software MatLAB al cálculo del mapa mensual de temperaturas medias para cada uno de los meses, y que a modo de ejemplo se muestra en la siguiente figura el correspondiente al mes de mayo.
 |
| Mapa de Temperatura media mensual del mes de mayo |
 |
| Evolución de los valores medios de temperatura por meses |
Las12 imágenes del mapa obtenido se pueden ver aqui.
Enlaces de interés:
Anterior: Carta bioclimática de Olgyay
Siguiente: Mapa mensual de Humedad Relativa
No hay comentarios:
Publicar un comentario